Tonality is highly charged system where scale degrees are endowed with a magnetic or gravitational pull towards other tones. Within the key of C major, B-natural is attracted to the tonic C, other members of the dominant triad are attracted to the tonic triad, and other scale degrees have functions as well. Spelling is extremely important within common-practice tonality. A-flat — as lowered scale degree 6 — leads to G, but G-sharp — as raised scale degree 5 — leads to A. Underlying “scale degree” and “spelling” are two important concepts that will influence our study of post-tonal music.

Octave Equivalence

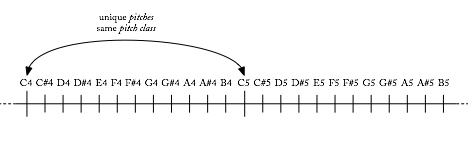
”Scale degree” implies an equivalence between pitches that are spelled the same but any number of octaves apart. C4 is the same as C3 is the same as C9, and so on. The concept of scale degree, then, has the idea of octave equivalence embedded within it.

Enharmonic Equivalence

Though octave equivalence is central to our understanding of tonal music, enharmonic equivalence often is not. In the key of C major, A-flat and G-sharp are not equivalent, though in isolation they sound the same. Spelling often indicates tendency: A-flat falls to G and G-sharp rises to A.

In post-tonal music, enharmonic equivalence is often assumed — with exceptions of course. Because many composers no longer felt constrained by a tonal center, the same gravitational relationships amongst tones that we find in tonal music aren’t important. A-flat and G-sharp, therefore, can be treated as representations of the same thing.

Pitch

Pitches are discrete tones with individual frequencies. The concept of pitch, then, does not imply octave equivalence. C4 is a pitch, and it is not the same pitch as C3.

Pitch class

Pitch classes are pitches under octave equivalence that are also spelled the same. A4, A3, A2, etc. are all members of the pitch class A.

Pitch Space

Integer notation

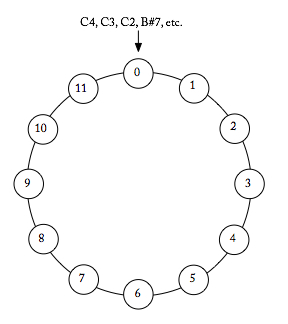
When analyzing post-tonal music where assuming octave equivalence and enharmonic equivalence is appropriate, we can use integers to represent pitch class. All C’s and any notes that are enharmonically-equivalent to C (B-sharp, for example) are pitch class 0. All C-sharps’s and any notes that are enharmonically-equivalent to C-sharp (D-flat, for example) are pitch class 1. And so on: C = 0, C-sharp = 1, D = 2, D-sharp = 3, E = 4, F = 5, F-sharp = 6, G = 7, G-sharp = 8, A = 9, B-flat = 10 (T), and B = 1 1 (E).

This type of pitch-class, which assumes octave and enharmonic equivalence is easily visualized on a clock-face diagram, like the one below.

Pitch-Class Space

Disclaimer!

Post-tonal music is extremely various. Composers have individual compositional styles, aesthetic goals, and unique conceptions of pitch. All this is to say that you must approach a composition with flexibility. For example: because it is quasi-tonal, Debussy’s music often benefits from a view that does not assume enharmonic equivalence. But sometimes it does. You must rely on your musical intuitions when analyzing this music, and you should also be willing to approach pitch in these compositions from multiple perspectives until you find one that seems most appropriate.